Binary systems: orbital period and mass transfer

M. Bonnardeau
30 Nov 2005

Abstract

The equations for the relation between the orbital period change of a binary system and the mass transfer are explicited.

Mass transfer and orbital period change

Let be a binary system with the masses of the stars M1 and M2 and M= M1+ M2. The stars are orbiting around their center of gravity at the distances R1 and R2 with R=R1+R2 and M1*R1=M2*R2. G is the gravitational constant.

The gravitational force between the two stars is balanced by the centrifugal forces:



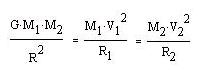
where V1 and V2 are the orbital velocities. Assuming the orbit is circular:



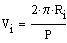
Then the orbital period:

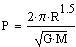
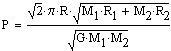
The total angular momentum is:

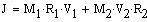
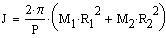
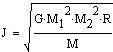
Matter is accreted from one star by the other. The mass transfer is assumed to be conservative, that is M'1=-M'2 (' is the derivative d/dt). The total angular momentum J is conserved. Then:



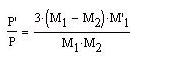
When the accretion is from the less massive star to the more massive star, the orbit becomes larger and the period increases.
When the mass transfer is the opposite way, the orbit shrinks and the period decreases.