Light-travel time effects in binary systems
Michel Bonnardeau
8 March 2007
Updated 6 May 2010 (close binary), 12 Feb 2021 (CK Aqr)
Abstract
The light-travel time effects for a pulsating star (or a close binary) in a binary system are calculated.
Introduction
A pulsating star (or a close binary) in a binary system seems to pulsate (or to rotate) faster as it moves towards Earth, and slower as it moves away. The observations of such variations may be used to calculate the orbital parameters.
An example is CK Aqr, a contact binary with a period of 6.8 h orbiting a third body with an orbital period of 8.2 yr.
Orbital parameters

The blue star M is less massive than the the green star. S1
is the center of gravity and the focus of the 2 elliptical orbits.
A is the periastron.
In a binary system, the two stars describe elliptical orbits (Kepler's first law).
Let be a
a the semi-major axis and b the semi-minor
axis of one of the ellipse. a and b are related to the eccentricity e by:
 | (1) |
Any point M of the ellipse obeys:
S1M+S2M = 2*a
where S1 and S2 are the foci,
with:
OS1=a*e
The equation of the ellipse is:
 | (2) |
Let be r the distance S1 and phi the angle from
the x axis (phi is the true anomaly). One has:
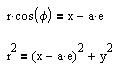
With (2) that gives:
 | (3) |
Let us determine phi as a function of the time t. According to Kepler's
second law, a line joining a star in a binary system and a focus sweeps
out equal areas during equal intervals of time, that is:
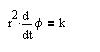
with k a constant. With (3) this gives:
 | (4) |
Let be P the orbital period. Then k can be determined from:

with (3) this gives:
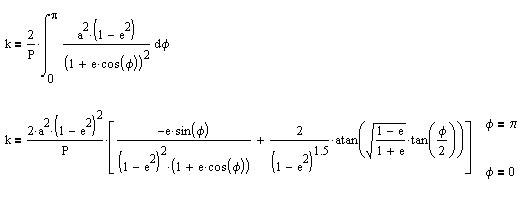
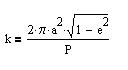
phi(t) can then be determined iteratively from:

or
 | (5) |
A simplified calculation (valid for e small)
When e is small, these equations may be simplified. (4) can be written
as:
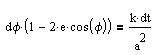
which gives:
 | (6) |
What is the effect of this approximation on the light-travel time (LTT)?
The LTT is of the order of:
LTT = (r/c)*sin(phi)
with c the velocity of light.
With a = 1 a.u., the difference between LTTapprox
and LTTexact is then:
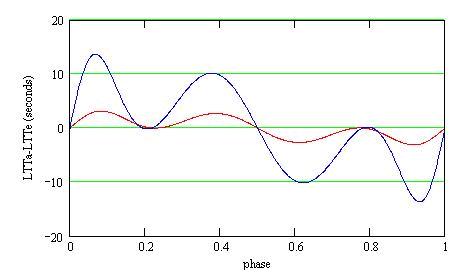
Red: eccentricity e=0.1, Blue: e=0.2.
Light-travel time
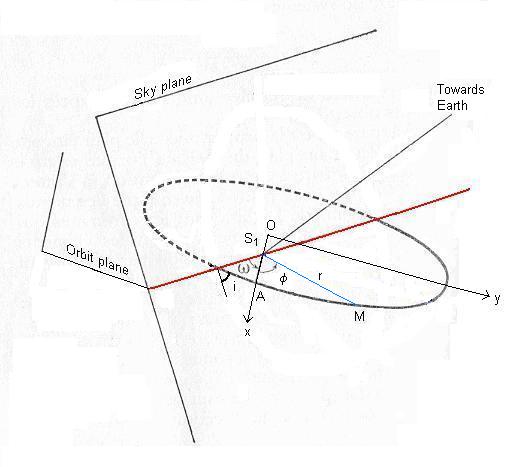
The node line in red is the intersection of the orbit plane with the
sky plane that goes through the focus S1.
The angle i between the two planes is the inclination: it is in
the [0°,90°] range when the orbit is direct i.e. when the projected motion on the
sky plane rotates in the trigonometric direction; it is in the [90°,180°] range
when the orbit is retrograde. omega is the angle between the node line and the major axis.
Let us assume that the orbiting object M emits pulsations. When these
pulsations are received by the observer, they are delayed by the light-travel
time effect:
 | (7) |
|
|
|||
|
|||
|
|
|||
|
|
|||
|
|||
