Relativity: a quick introduction

Michel Bonnardeau

3 Jan 2015
Revised 28 Feb 2016

Abstract

A quick introduction to Special Relativity with a derivation of E=mc2.

1. Electromagnetism

Let be two electric charges q₁ and q₂ separated by a distance r, in the vacuum. The electrostatic force F between them is:

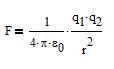
where ε₀ is the electrical permittivity, a constant that tells how the electric field propagates in the vacuum.

Let be two parallel wires of length l, separated by a distance r, which carry the currents of intensities I₁ and I₂. The length l is much greater than the distance r. The magnetic force F, in the vacuum, between the two wires is:

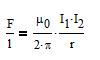
where μ₀ is the magnetic permeability, a constant that tells how the magnetic field propagates in the vacuum.

The 4.π.r² for the electrostatic force and the 2.π.r for the magnetic force come from the geometry: in one case the electric field goes through a sphere of surface 4.π.r², in the other the magnetic field goes through a cylinder of surface 2.π.r.l (when l>>r).

The dimension of the electric permittivity is [ε₀]=force^-1.charge².length^-2 and the one of the magnetic permeability is [μ₀]=force.intensity^-2. With the dimension of the intensity being that of a charge/time, the dimension of (ε_0.μ₀)^-1/2 is that of a velocity.

In 1862, Maxwell derived a set of equations connecting the electric and magnetic fields (the "Maxwell's equations") and showed that an electric field and a magnetic field may propagate in the vacuum with the velocity (ε_0.μ₀)^-1/2. In 1887, Hertz realized the first man-made radio transmission with these electromagnetic waves.

The permittivity and the permeability may be measured experimentally:
ε₀ = 8.854...*10^-12 MKS
μ₀ = 12.566...*10^-7 MKS
then:
(ε_0.μ₀)^-1/2 = 299.8...*10⁶ m/s.
(ε₀.μ₀)^-1/2 is equal to the velocity of light. One may guess this is no coincidence and that light is an electromagnetic wave.

1.1. A velocity relatively to what?

The Maxwell's equations do not say in which frame the velocity (ε_0.μ₀)^-1/2 is.

Let us consider a pedestrian walking at 4 km/h on the ground. If he walks in a train speeding at 100 km/h (over the ground), then the pedestrian velocity, relatively to the ground, is either 104 or 96 km/h depending upon if he walks towards the head or the tail of the train.

However, the measurements of ε₀ and μ₀ onboard the speeding train are not expected to be different from the ones on the ground and, above all, the idea of measuring them towards the head or the tail of the train does not make sense.

1.2. The ether

The idea is that the velocity (ε_0.μ₀)^-1/2 is within a special frame called the ether. If someone moves at the velocity v within the ether and emits a beam of light in the direction of the motion, the velocity of the light is (ε_0.μ₀)^-1/2+v.

Michelson and Morley designed an experiment to check this idea: the Earth circles the Sun with a velocity v=30km/s. Let us assume that the Sun is stationary in the ether (if it is not, the calculations are more complicated but the reasoning is the same). If one measures the velocity of light in the direction of motion of Earth it should be (ε_0.μ₀)^-1/2+v, in the opposite direction (ε₀.μ₀)^-1/2-v, and (ε₀.μ₀)^-1/2 in the perpendicular directions. Michelson and Morley built an interferometer to measure the differences between those velocities. And the result was negative: the velocity of light was observed to be the same in all directions.

2. Relativity

In 2005, Einstein published the theory of Relativity. The basic idea is that if the equations of Maxwell do not specify the frame of the velocity (ε_0.μ₀)^-1/2, it is because it is the same in all the frames. There is no need for the ether.

This was a revolutionary idea. A velocity is a distance divided by a time. A distance is measured with a rule, a time with a clock. For the velocity of light to be the same in any frame, space and time must be related in some way.

Let be c:

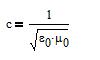
This is a characteristic velocity of spacetime, rather than the velocity of light. Light, actually, takes this velocity (and so should gravitational waves).

During the time interval dt, light travels the distance (dx²+dy²+dz²)^1/2=c.dt in some frame. Then the quantity ds²=c²dt²-dx²-dy²-dz² is 0. In another frame, with the velocity of light still c, one still has ds'²=c²dt'²-dx'²-dy'²-dz'²=0. Note that dt' is allowed to be different from dt.

For any object in spacetime one may calculate ds²=c²dt²-dx²-dy²-dz². It has to be greater or equal to 0, because it is a square. As with light, it is considered to be an invariant from one frame to another in a uniform motion relatively to the original one, i.e. ds'²=ds². ds² is a square and cannot be negative, then c is the maximum allowed velocity.

2.1. The transformations of Lorentz

Let be two frames (S) and (S') with their respective axes parallel and in motion relatively to one another with a constant velocity v. The orientation and origin of the axes is such that the motion is along the x and x' axes and the coordinates of the origin of (S') in (S) is x=v.t, y=0, z=0.

Let be u=i.c.t. Then du²+dx²+dy²+dz²=-ds² is an invariant (the same in (S) and (S')). With the motion along the x (x') axis, this is equivalent as being invariant in a rotation in the (x,u) plane.

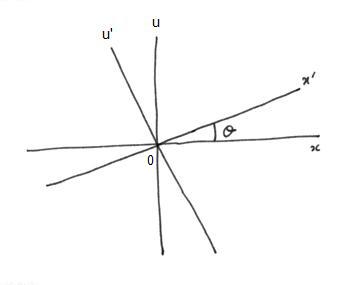
Let be θ the angle of rotation between (x,u) and (x',u'). One has
x'=x.cosθ+u.sinθ
u'=-x.sinθ+u.cosθ

The origin of (S') is x'=0 and x=v.t. This gives:

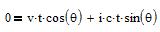
then

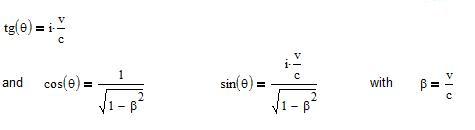
This gives the "transformations of Lorentz":


and the inverse transformations:

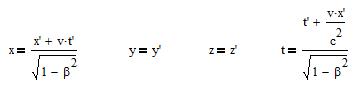
The time t' in the frame (S') is different from the time t in the frame (S). However, when the velocity v is very small compared to c, one finds the classical relations:
x'=x-v.t
t'=t

2.2. Simultaneity

Let be two events at (x₁,y₁,z₁,t₁) and (x₂,y₂,z₂,t₂) that are simultaneous in the frame (S), i.e. t₁=t₂. In the frame (S') one has:

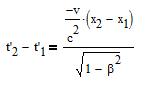
that is different from 0, so the events are not longer simultaneous in (S').

Again, when v<<c, one has t'₁=t'₂ and the events are simultaneous.

However, causality is conserved. When the event 1 at (x₁,y₁,z₁,t₁) triggers the event 2 at (x₂,y₂,z₂,t₂) (t₁<₂) in (S), one has in (S'):

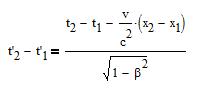
For causality to be violated in (S') (t'₁>t'₂), one would need:

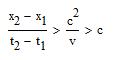
i.e. a faster than c velocity between 1 and 2.

2.3. Time dilatation

A clock at (x,y,z) measures the duration t₂-t₁ in the frame (S). In the frame (S') one has the duration:

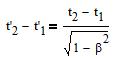
The time goes slower in (S') than in (S). This leads to the twin paradox: let be two twin sisters. One moves away. The one who stays ages faster than her sister.

2.4. Length contraction

Let be a stationary rule in (S'), parallel to the x' axis. Its length is L'=x'₂-x'₁. Its length L at time t in (S) is then:

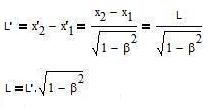
The length is shorter in (S) than in (S').

The first experimental tests of time dilation and length contraction were done with muons. A muon is an unstable elementary particle that decays with a period P=2.2μs. That is, if one has a population of a number of muons at rest, half of them have decayed after a time interval of P.

Let us consider a population of muons traveling at a velocity very close to c. According to Classical Mechanics, only half of them should remained after traveling a distance c.P. Actually many more are observed:
let be (S) the referential of the observer,
and (S') the one of the muons.
The period P is in (S'). In (S) it is P.(1-β²)^-1/2, greater than in (S');
or: the travel length for half the muons to decay is c.P in (S'). In (S) it is c.P.(1-β²)^-1/2, longer than in (S').

2.5. Composition of velocities

Let be V the velocity of an object in (S). V is a vector with the (V_x,V_y,V_z) components along the (x,y,z) axes. In (S') the velocity is V' with the components (V'_x,V'_y,V'_z):

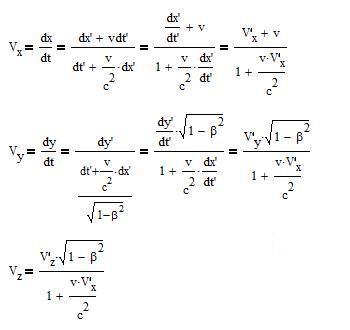
and the reverse transformations, obtained the same way:

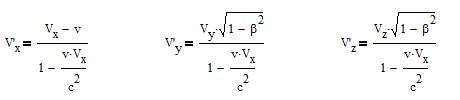
When v<<c one finds the classical expressions:
V_x=v+V'_x
V_y=V'_y
V_z=V'_z

and with V_x=c, V_y=0, V_z=0 one finds:
V'_x=c
V'_y=0
V'_z=0

3. Inertia

In Classical Mechanics, the principle of inertia states that the velocity V of an object stays constant if it is not submitted to any force, that is:
dV/dt = 0

In Relativity, the above expression is not invariant from one referential to another one in translation, because dt' is different from dt. So one needs another equation.

Let us start from the invariant ds:

ds² = [c²-(dx²+dy²+dz²)/dt²]dt² = (c²-V²)dt² = c²(1-β²)dt²

with β=V/c. Let be the "proper time" dτ = (1-β²)^1/2dt. ds=c.dτ. As ds is an invariant, so is dτ. The principle of inertia in Relativity is then considered to be:
dV/dτ = 0

3.1. The 4-velocity

Let us introduce the "4-velocity": u = ds/dτ where ds has the components (dx,dy,dz,cdt). One has:

u = (ds/dt)(dt/dτ) = (ds/dt)(1-β²)^-1/2

with the four components:

u_x = V_x(1-β²)^-1/2   u_y = V_y(1-β²)^-1/2   u_z = V_z(1-β²)^-1/2
u_t = c(1-β²)^-1/2

The velocity with the components (u_x,u_y,u_z) is the "proper velocity".

4. The equation of dynamics

In Classical Mechanics, the force F applied to an object of mass m is related to its acceleration dV/dt by the equation of dynamics:
m.(dV/dt) = F

In Relativity, this law is rewritten as:
m.du/dτ = φ
where u is the proper velocity, τ the proper time and φ will be explained below. This can be rewritten as:
m.(du/dt) = φ(1-β²)^1/2
or

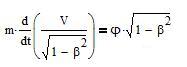
One gets back to Classical Mechanics when β is small by identifying:
F = φ.(1-β²)^1/2
Then the Einstein's equation of dynamics:

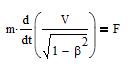
4.1. Relativistic mass

The equation of dynamics may be written as
F = dp/dt
where p is the momentum. p=m.V in Classical Mechanics.

From the above relativistic equation of dynamics, one has:

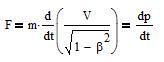
with

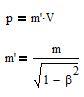
m' is the relativistic mass. If m is different from 0, m' is equal to m if V=0, it increases with V, and it becomes infinite if V becomes equal to c.

Experimentally, for a particle accelerator to work (e.g. a synchrotron to accelerate protons or electrons up to a velocity close to c), this increase of the mass of the accelerated particles, as seen from the accelerator, must be taken into account.

5. Energy

The energy necessary to give to an object, starting at rest, a velocity V by applying a force F on it, is:

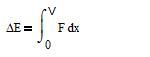
where x is the displacement of the object. This may be rewritten as a function of the momentum p:

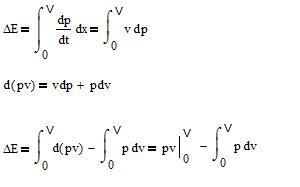
With m the rest mass of the object:

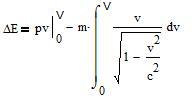
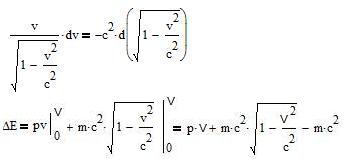
One has ΔE=E(V)-E with E(V) the energy of the object at the velocity V and E=m.c² its energy at rest.

When the velocity v becomes very small, one gets back to Classical Mechanics:
ΔE = (1/2).m.V²

So, Relativity implies that there is an energy associated with a mass at rest, E=m.c², or that mass and energy are equivalent. Furthermore, this equivalent energy of a mass is enormous: 1 kg of matter holds 9.10¹⁶ J. That is about the energy produced by a nuclear power reactor during one year (1 GW output of electricity, with a yield of 1/3).

Experimentally, this equivalence of mass and energy is verified in particle physics, when one study the output (the masses of the outgoing particles and their kinetic energy) of the interaction of two particles. And also in nuclear physics. In chemistry, the energy produced in a chemical reaction is so small that the corresponding loss of mass is practically undetectable, so the old Lavoisier's law (nothing is created, nothing is lost) is still a valid approximation.

6. Conclusions

This quick introduction was about Special Relativity, dealing with frames in uniform motion relatively to one another. There is also the General Relativity, dealing with frames in acceleration relatively to one another, and leading to an elegant description of gravity, with fundamental implications in cosmology.

All the consequences of Relativity are verified experimentally. Relativity is no longer the "Theory" of Relativity but rather the Relativistic "Mechanics".

Before the discovery of Relativity, space and time were thought to be unrelated, and that an object might travel with an unlimited velocity. Special Relativity shows that:
-space and time are related;
-there is a speed limit c;
-mass and energy within this spacetime are equivalent.

These properties and limitations of spacetime suggest that spacetime is actually some kind of something. And this does not stop with Special Relativity:

According to General Relativity, spacetime is curved by mass/energy (leading to gravitation). And the universe, including its spacetime, did have a beginning and have been expanding since then.

It is observed that the universe is undergoing an accelerated expansion and it seems (this is not firmly established yet) that this acceleration is an unexplained property of spacetime itself (is not due to something within spacetime).

According to Quantum Mechanics, a particle may not be localized within spacetime, i.e. it may not have acquired x,y,z,t coordinates and be actually everywhere.