Transformations for differential photometry
M. Bonnardeau
28 May 2007
Abstract
An introduction to transformation coefficients and equations for differential photometry.
The transformation equations
The transformation is a correction to differential photometry measurements to take into account the instrument (telescope, filter, camera) and atmospheric transmission. This transformation can be made when two filters are used, for example the B,V filters.
For this, the transformation coefficients Tbv and Tb are necessary:
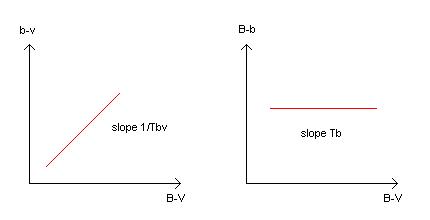
B,V are the exact magnitudes, b,v are the measured magnitudes. A first
order approximation is to assume that the responses of the setup (instrument
+ atmosphere) are linear. Then Tbv and Tb are constant slopes. For a perfect
setup, Tbv=1 and Tb=0.
The astronomer uses a comparison star with known magnitudes Bc,Vc and
measures the magnitudes b,v for a star. One wants the transformed magnitudes
B,V. One has:
| b-v = (1/Tbv)*(B-V)+cst | (1) |
| B-b = Tb*(B-V)+cst | (2) |
This gives:
| B-V = Tbv*(b-v)+k1 | (3) |
| B-b = Tb*Tbv*(b-v)+k2 | (4) |
with k1 and k2 constants. For the comparison star, (4) gives:
0 = Tb*Tbv*(Bc-Vc)+k2
Then the transformation equation:
| B = b+Tb*Tbv*[(b-v)-(Bc-Vc)] |
For the comparison star, (3) gives:
Bc-Vc = Tbv*(Bc-Vc)+k1
Then:
| V = B-(Bc-Vc)-Tbv*[(b-v)-(Bc-Vc)] |
A variant:
Instead of Tb one may use Tv:
0ne gets then the transformation equations:
| V = v+Tv*Tbv*[(b-v)-(Bc-Vc)] |
| B = V+(Bc-Vc)+Tbv*[(b-v)-(Bc-Vc)] |
Derivation of the transformation coefficients
A field of several stars whose magnitudes are precisely known is observed. Usually this is a
Landolt's standard field. The intensities of these stars
are measured and fitted with Pogson's law:
The measured magnitudes of the stars are then derived.
The transformation coefficients Tbv and Tb can be derived by fitting
the measurements with linear functions:
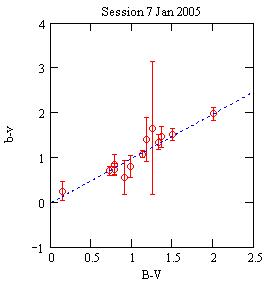
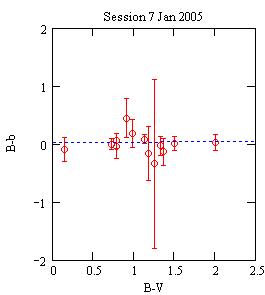
Actual observations of the field L95 that give Tbv=1.008 and Tb=0.008.

To determine Tbv, one wants to minimize:
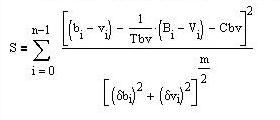
where Cbv is a constant. The denominator is a weight factor: the larger
the error on a measurement, the less it contributes to the determination
of Tbv. (The errors on B,V are negligeable). I use m=1.
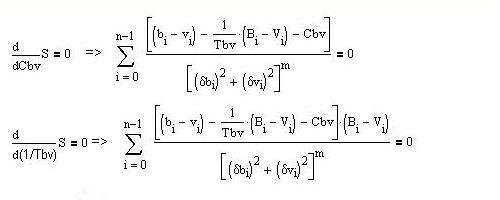
This gives:
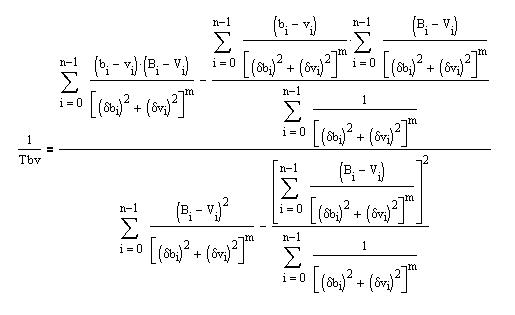
To determine Tb, one minimizes:
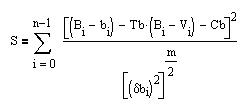
with Cb a constant. The result is:
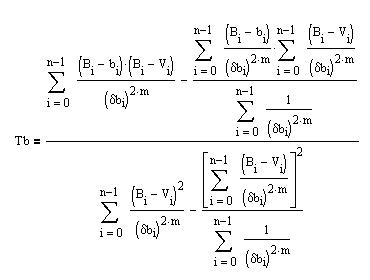
The wider the B-V range of the field, the better is the determination of the slopes and of the transformation coefficients.
Actual derivation of the coefficients
The transformation coefficients for my setup:
B, V transformations
V, Rc transformations
V, Ic transformations.
Link
B. Gary's web page on CCD transformations equations for use with single image photometry.
Another method
Another method is to derive the uncertainties on the coefficients and to use them as weights to compute the averages and standard deviations.
|
|
|||
|
|||
|
|
|||
|
|
|||
|
|||
