MBCAA Observatory

V1412 Aql: a simulation

Michel Bonnardeau
24 Aug 2009

Abstract

A Monte Carlo simulation which may be useful to search for eclipses is proposed.

Introduction

The white dwarf G24-9 (or V1412 Aql) was observed to be unexpectedly dim on 2 occasions, in 1985 and 1988. This is interpreted as eclipses due to a dark, substellar companion (Zuckerman & Becklin (1988)).

Feb 2009, the AAVSO lauched a campaign to observed this object to detect its eclipses (AAVSO Special Notice #148).

I propose here a Monte Carlo simulation which may be useful to speed up the discovery of eclipses.

Observations

The 2 observed eclipses are:

19851007.11 (Landolt (1985)), heliocentric correction 180.56s, t85=2446345.612 HJD;

19880715.3 (Carilli & Conner (1988)), heliocentric correction 441.74s, t88=2,447,357.805 HJD.

The AAVSO has 271 negative (i.e. no eclipse) observations on 23 Aug 2009.

Simulation

The orbital period is P=(t88-t85)/n where n is an integer.

G29-4 is a white dwarf, so it has a small size (about that of Earth), then the eclipse duration tau is given mostly by the diameter D of the occulting body:

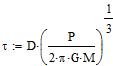
with M the mass of the system, G the gravitational constant (taking for the inclination i=90° and for the eccentricity e=0).

The computer simulation is a Monte Carlo one where a large number of random sets of n, M, D are used to derived ephemeris. The ephemeris that are retained are those that give the 2 observed eclipses and that do not give eclipses for the negative AAVSO observations.

The algorithm works the following way:

1,000,000 random sets of n, M, D are generated, with n between 1 and 100, M between 0.1 and 2 solar masses, D between 0.08 and 5 jovian diameters;

for each set the period P0=(t88-t85)/n and the eclipse duration tau is computed;

the ephemeris is HJD(E)=T+P*E with T an random number between t85-tau and t85+tau, and P a random number between P0-tau/n and P0+tau/n;

the ephemeris than do not give the eclipses at t85 and t88 are rejected;

the ephemeris that give an eclipse for one of the negative AAVSO observations are rejected.

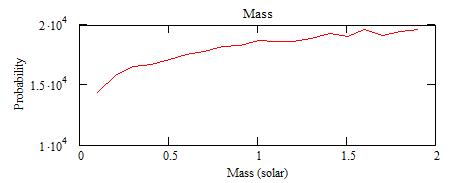
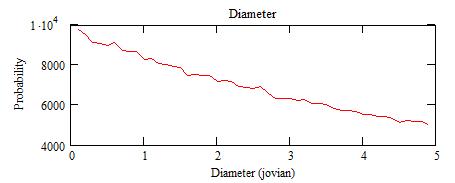
~~About 1/3 of the random sets give acceptable solutions~~. The spectra of n, M and D solutions are:

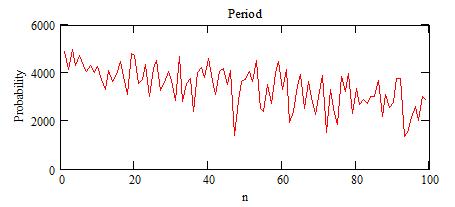
The "probability" is actually the number of acceptable solutions from the simulation.

The probability for the eclipse duration:

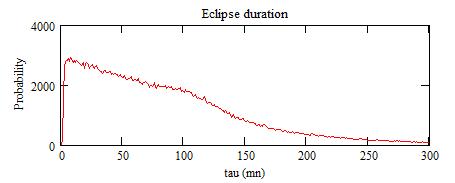
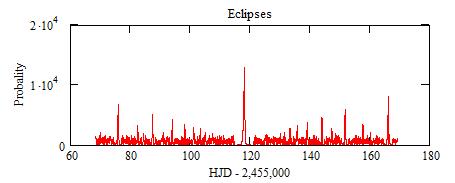
The probability for future eclipses may be computed:

Close-up:

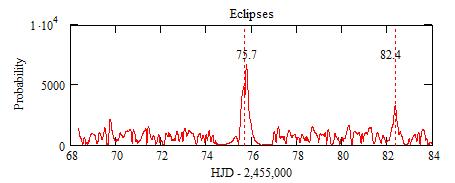
The peak around 75.7 (1 Sep 5hTU) comes from solutions with values of n that are multiple of 8. If indeed the period is given by n=8 or n=16, etc., a time-series around this date will pick up an eclipse. If not, this will eliminate all these solutions.
The peak around 82.4 (7 Sep 21hTU) comes from values of n that are multiple of 19. Again a time-serie will pick up an eclipse if n=19, 38, etc. or will eliminate these solutions.

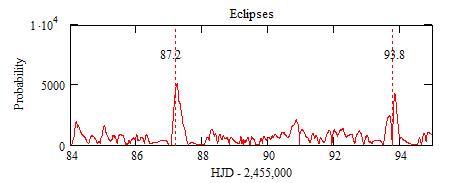
The peak around 87.2 (12 Sep 17hTU) comes from values of n that are multiple of 11, and the one around 93.8 (19 Sep 7hTU) from values multiple of 14.

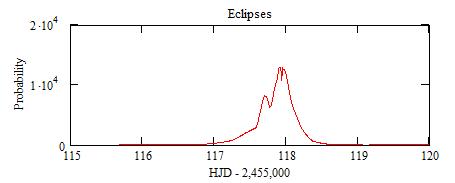
This large peak between 117 and 118.5 (12 Oct 12hTU and 14 Oct 0hTU) comes from values of n that are multiple of 3.