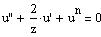Stellar structure

M. Bonnardeau
5 March 2006

Abstract

The equations that describe a polytropic star structure are derived.

Introduction

The equations to describe the structure of a star in a simple model are derived. This allows to compute the density, the pressure, the temperature as a function of the distance to the star center.

This note is to be used in another notes on pulsating stars.

Derivation of the state equation

First, let us consider the gravitational forces acting on any point A inside a star. The density depends only on the radius (and not on the directions). There are 3 forces:

Now, let us consider a cylinder at distance r from the star center, with a base area dA and a height dr. The forces acting on the cylinder are the pressure forces P(r)*dA and P(r+dr)*dA, and the gravitational pull of the mass Mr encompassed by the radius r and the star is in equilibrium:

where rho is the density and G the gravitational constant

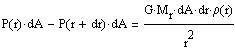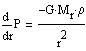(1)

Let us introduce the gravitational potential PHI:

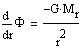(2)

With

(3)

one immediatly obtains:

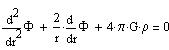	(4)
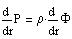	(5)

(4) is the Poisson equation.

Let us make a simplification and assume that the pressure and the density are connected the following way:

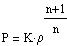(6)

where K and n are constant. Such a star model is called a polytrope and n is the polytropic index.

From (2) and (6) one has:

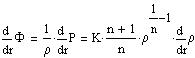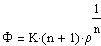	(7)
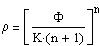	(7a)

with PHI=0 at the star surface where rho=0.

In the Poisson equation (4), this gives:

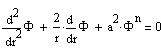	(8)
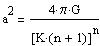	(8a)

Let us introduce the new variables z and u(z):

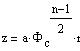	(9)
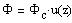	(10)

where PHIc is the gravitational potential at the star center. The Poisson equation (4) becomes, where prime ' is the derivative d/dz:

(11)

this is the Lane-Emden equation. This equation can be solved analytically for n=0 and n=1; it has no solution for n=5 and greater; it can be solved only numerically for other values of n.

To obtain the star structure, that is the density or the pressure as a function of the distance to the star center, the Lane-Emden equation is to be solved numerically (with the boundary conditions u(0)=1 and u'(0)=0). The density and the pressure are connected to u(z) the following way:

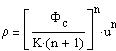	(12)
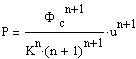	(12a)

with r and z connected by (9).

The temperature

Let be X and Y the proportions of hydrogen H and helium He (in mass, i.e. X is the mass of H in gram in 1 gram of star matter). The elements other than H and He are neglected. The star being completly ionized, the average mass of a star particle (H nuclei, He nuclei, electron) in unit of hydrogen mass is:

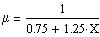(13)

For an ideal gaz, the gaz pressure Pgaz as a function of the temperature T is given by:

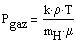(14)

where k is the Boltzmann constant and mH is the mass of an atom of H.

The radiation pressure Prad is:

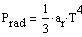(15)

where ar is the radiation constant, ar = 4*sigma/c, with sigma the Stefan-Boltzmann constant and c the velocity of light.

The pressure P inside the star is the sum of the gaz pressure and of the radiation pressure:
P = Pgaz+Prad

The Sun

Assuming the polytropic index is n=3 and knowing the H abundance X, let us give a central density and a given central temperature. The radius of the star and its mass may then be computed: the radius is given by z such as u(z)=0 and by (9), and the mass is:

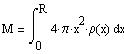
At the surface of the Sun the H abundance is observed to be X=0.744 and is assumed to be constant with the distance to the center. The radius of the Sun is Ro=700,000km and its mass is Mo=2E33g. By trial, I find that these values can be reproduced with a central density of 78g/cm3 and a central temperature of 11.8E6°K. The central pressure is then 1.3E17dynes/cm2, mostly due to the gaz. The internal structure is:

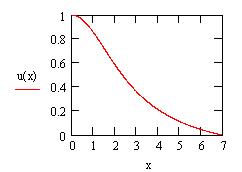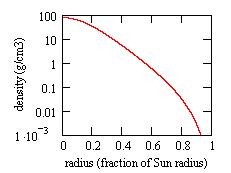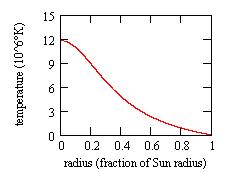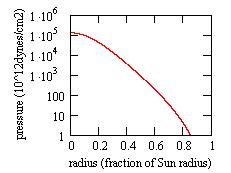Actually more sophisticated models of the Sun give (Harvey (1995)):

rhooc = 156 g/cm3
Toc = 15.8E6 °K
Poc = 2.4E17 dynes/cm2

Therefore the simple model presented here gives realistic results. A more sophisticated model would take into account, among other things:

More

Stars can oscillate around their equilibrium position: see the next astronomical note Pulsating stars I: differential equation.

This modelling does not apply to non-gazeous stars, i.e.:

Reference

Harvey J. (1995) Physics Today Oct 32 Helioseismology.