Pulsating stars I: Differential equation
M. Bonnardeau
24 Feb 2006
Abstract
The differential equation of a radially pulsating star is derived.
Introduction
If you know how to derive the differential equation of an oscillating
spring and to calculate its period, this should be enough to understand
this elementary introduction at computing the radial pulsations of a star.
 |
 |
 |
In this note (Part I), the differential equation for a radially pulsating
star is derived;
Part II the pulsation periods are computed in the simple case
of a constant density star;
Part III a more realistic polytropic star model is considered.
Derivation of the differential equation
First, let us consider the gravitational forces acting on any point
A inside a star. The density inside the star depends only on the radius
(and not on the directions). There are 3 forces:
It can be demonstrated that the gravitational forces from the yellow and the green region exacly compensate and that we are left with only the pull from the orange sphere. This is the Newton theorem (similar with the Gauss theorem of electrostatic).
Now, let us consider a cylinder at distance r from the star center, with
the base area dA and the height dr. The forces acting on the cylinder
are the pressure forces P(r)*dA, P(r+dr)*dA and the gravitational pull
of the mass Mr encompassed by radius r. They are equal to the mass of
the cylinder times its acceleration:
 |
where rho is the density and G the gravitational constant. With
 |
(1) |
it comes:
 |
(2) |
Let us consider the perturbations, assumed to be small:
 |
(3) |
 |
(3a) |
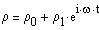 |
(3b) |
putting them in (1) gives:
 |
|
 |
(4) |
 |
(5) |
The gravitational acceleration is:
 |
(6) |
then putting the perturbations in (2) gives:
 |
|
 |
(7) |
 |
(8) |
With an ideal gaz, the pressure reacts to a change of density the following
way:
 |
(9) |
with gamma a constant (gamma=5/3 for an adiabatic gaz, i.e. that does not exchange heat with its surrounding).
The differential equation for the variations of r1
as a function of the pressure P0 and of the density
rho0 can now be readily derived. Let us introduce
the new variables X and p:
 |
(10) |
 |
(11) |
Putting this in (4) and (5) gives, with prime ' for d/dr0:
 |
|
 |
|
 |
|
 |
(12) |
and with (7) and (8):
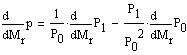 |
|
 |
|
 |
(13) |
Deriving (12) gives:
 |
(14) |
and with (13) we obtain the differential equation for the star radial pulsations:
|
(15) |
Part II the pulsation periods are computed
in the simple case of a constant density star;
Part III a more realistic polytropic star model is considered.
|
|
|||
|
|||
|
|
|||
|
|
|||
|
|||

