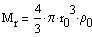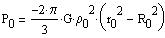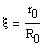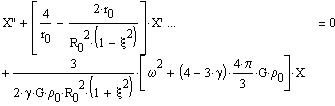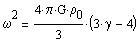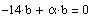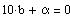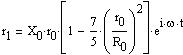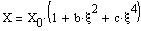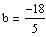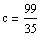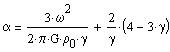Pulsating stars II: Solutions at constant density

Michel Bonnardeau
24 Feb 2006
Revised 13 July 2012

Abstract

The differential equation for a radially pulsating star is solved for a constant density.

Introduction

Part I the differential equation of a radially pulsating star was derived.

Let us now make the simplification that the density of matter is constant throught the star (a "liquid" star). The differential equation (15) of Part I is then easily solved. Although this may look grossly oversimplified, we will see that the results are meaningful.

The differential equation for a "liquid" star

With the density rho0 constant:

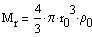	(1)
	(2)

This gives from equations (1) and (7) of Part I:


Let us introduce, where R0 is the radius of star:

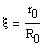(3)

The differential equation (15) of Part I may then be written:

(4)

with

(5)

or

Fundamental mode solution

An obvious solution to equation (19) is X=constant and alpha=0. The star oscillation is then:

	(6)
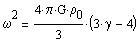	(7)

For the oscillation to be stable, one needs gamma>4/3. If gamma is smaller the star is instable: a small perturbation makes it collapse or blow up. (gamma=4/3 is for a radiation pressure dominated gaz).
With an adiabatic gaz, gamma=5/3 and the oscillation is stable.

The pulsation period is:

(8)

Let us consider the Sun as being of constant density. With a mass of 2*10^33g, a radius of 700,000km, the density is then 1.39g/cm3 and the computed pulsation period is 168mn. The Sun is observed with many oscillations, from a 160mn period down to a 5mn period. The computed period happens to be very close to the 160mn period.

More realistic models of the Sun lead to smaller periods. For example the polytropic n=3 model gives a period of 55mn for the fundamental mode. So the liquid star model gives only the right order of magnitude.
The observed, weak (21cm/s), 160-mn period oscillation of the Sun is NOT the fundamental oscillation mode, and is not that easily explained.

With a Cepheid of 5 solar masses, and a radius of 60 solar radii, the computed pulsation period is 24 days. This is a typical observed pulsation period for this kind of star.

First overtone solution

Let search a solution to (19) of the form


the differential equation (19) becomes


this gives


The oscillations are then of the form

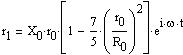(9)

with the period given by:

(10)

Second overtone solution

With a solution of the form:


one has:


with the period given by:

(11)

Oscillation amplitudes

The amplitudes of the oscillations as a function of the distance from the star center:


Red: fundamental mode, Blue: 1st overtone, Magenta: 2nd overtone.

More

Part III: solutions to the differential equation of the oscillations from a more realistic, polytropic model of the star structure are presented.