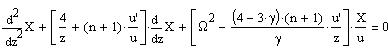Pulsating stars III: Polytropic model

Michel Bonnardeau
6 March 2006
Revised 13 July 2012

Abstract

The solutions to the differential equation of a radially pulsating star are presented for a polytropic model.

Introduction

Part I was written down the differential equation for the oscillations of a pulsating star;
Part II this equation was solved in the case where the star density is constant; This part, a more realistic model of the star is used.

Differential equation for the pulsations from the Lane-Emden function

Part I was established the differential equation for the pulsations:

I-(15)

where r0 is the distance from the star center,
r1 is the amplitude of the oscillation and X=r1/r0,
prime ' is the derivation d/dr0,
rho0 is the density at r0,
P0 is the pressure at r0,
g0 is the gravitational acceleration at r0 (see I-(6)),
gamma describes the P response to a change of density (gamma=5/3 for an adiabatic ideal gaz),
omega is the pulsation of the oscillation.

In the astronomical note Star structure (referred as "S" here) the density and pressure are computed as a function of the distance r0 from the star center for a polytropic model, using the Lane-Emden function u(z):

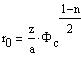S-(9)

where PHIc is the gravitational potential at the star center,

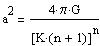S-(8a)

and n is the polytropic index:

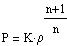S-(6)

The density and the pressure are given by:

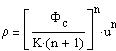	S-(12)
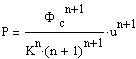	S-(12a)

Although both gamma and n relate the pressure to the density, they are not to be confused:

One has, with u'=du/dz:



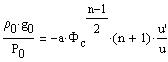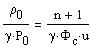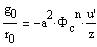Putting these into the differential equation I-(15) gives:

(1)

(1a)

OMEGA depends only on the indexes n and gamma (the Lane-Emden function u(z) depends only upon n). It does not depend upon the other parameters of the star such as its mass, etc.
The star is unstable for gamma<4/3 and the period of the fundamental mode is infinite when gamma=4/3. (gamma=4/3 is when the pressure is dominated by the radiative pressure). The periods depend only on the density at the center of the star:

	(2)
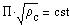	(2a)

The Q-value or pulsation constant: The density at the center is expected to be proportional to the average density rhom which may be directly observed from the star mass and radius. Pulsating stars are then quite often characterized by their observed Q-value:

(3)

with the period PI in days and rhomo the average Sun density.

Schwarzschild solution

Equation (1) was solved numerically by Schwarzschild (1941) for the polytropic index n=3, up to the fourth overtone, and for different values of gamma. The ratios of the overtone periods to the fundamental period are:

gamma	10/7 = 1.43	20/13 = 1.54	5/3 = 1.67 adiabatic
PI1/PI0	0.554	0.687	0.738
PI2/PI0	0.402	0.515	0.570
PI3/PI0	0.317	0.412	0.461
PI4/PI0	0.262	0.343	0.387

and the ratios of the successive overtone periods (for gamma=4/3 the fundamental period is infinite):

gamma	4/3 = 1.33 radiative pressure	10/7 = 1.43	20/13 = 1.54	5/3 = 1.67 adiabatic
PI1/PI0	0.000	0.554	0.687	0.738
PI2/PI1	0.700	0.724	0.749	0.772
PI3/PI2	0.778	0.789	0.799	0.810
PI4/PI3	0.822	0.828	0.833	0.839

The dependance of the pulsations with the polytropic index n for gamma=5/3 (Cox (1967)):

n	PI1/PI0	Q
n=0 liquid star model	0.28	0.1158
n=1.5 convective model	0.465	0.0703
n=3 standard model	0.738	0.0383

More

Non radial oscillations: They are characterized by their degree and azimuthal orders:

The l,m,n oscillations of the Sun are well observed (although they have much smaller amplitudes than for a "variable" star) and much studied (helioseismology). This allows a good understanding of the structure and of what is going on inside the Sun. This brought up the "solar neutrino problem": early neutrino telescopes detected much less neutrinos than predicted by these Sun models. The explanation was found recently (2002 Nobel Prize): the neutrinos switch from one specie into another.

p-mode and g-mode: the restoring force for the oscillations studied here is the pressure: these oscillations are p-mode waves. Other oscillations may be due to buoyancy: they are gravity mode or g-mode waves. g-mode waves cannot travel through convection zones; the external layer of a star being usually convective (because of the strong temperature gradient), they are then trapped in the deep interior.

References

Cox J.P. (1967) IAU Symposium n°28 p3

Schwarzschild M. (1941) ApJ 94 245.