V1412 Aql: a simulation

Michel Bonnardeau
First version 24 Aug 2009
Updated 2 Sep 2009 (more observations)
Updated and corrected 3 Sep 2009 (more observations; uncertainties on the ToM of the 2 eclipses taken into account at the suggestion of Wolfgang Renz; correction of the number of solutions)
Updated 5 Sep 2009 (more observations; simulation with the period down to 1 d; inclination)
Corrected 10 sep 2009 (uncertainties on the ToM of the 2 eclipses)

Abstract

A Monte Carlo simulation which may be useful to search for eclipses is proposed.

Introduction

The white dwarf G29-4 (or V1412 Aql) was observed to be unexpectedly faint on 2 occasions, in 1985 and 1988. This is interpreted as eclipses due to a dark, substellar companion (Zuckerman & Becklin (1988)).

Feb 2009, the AAVSO lauched a campaign to observed this object to detect its eclipses (AAVSO Special Notice #148).

I propose here a Monte Carlo simulation which may be useful to speed up the discovery of eclipses.

Observations

The 2 observed eclipses are:

19851007.11 (Landolt (1985)), heliocentric correction 180.56s, t85=2,446,345.612 HJD. The uncertainty is taken as et85=0.005 HJD;

19880715.3 (Carilli & Conner (1988)), heliocentric correction 441.74s, t88=2,447,357.805 HJD. The uncertainty is taken as et88=0.05 HJD.

The AAVSO has 600 negative (i.e. no eclipse) observations on 1 Sep 2009.

Arne Henden obtained 14 time-series showing no eclipses, from 30 Oct to 8 Dec 2008, total duration 34.1 h. And also 7 short time-series, in 2002 and 2008, total duration 2.6h.
Robert Fridrich obtained a time-series on 1 sep 2009, duration 0.3 h.

Simulation

The orbital period is P=(t88-t85)/n=(1012.193 days)/n where n is an integer.

G29-4 is a white dwarf, so it has a small size (about that of Earth), then the eclipse duration tau is given mostly by the diameter D of the occulting body:

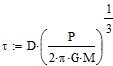
with M the mass of the system, G the gravitational constant (taking for the inclination i=90° and for the eccentricity e=0).

The computer simulation is a Monte Carlo one where a large number of random sets of n, M, D are used to derived ephemeris. The ephemeris that are retained are those that give the 2 observed eclipses and that do not give eclipses for the negative AAVSO observations.

The algorithm works the following way:

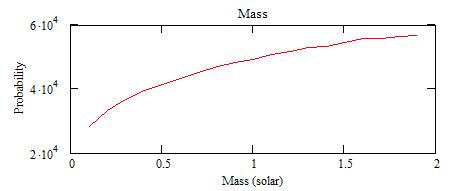
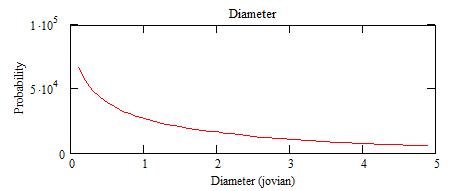
The spectra of n, M and D solutions are:



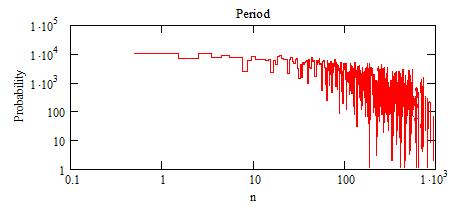
The "probability" is actually the number of acceptable solutions from the simulation.

The probability for the eclipse duration:



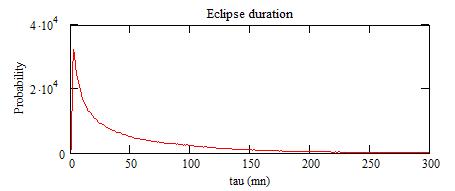
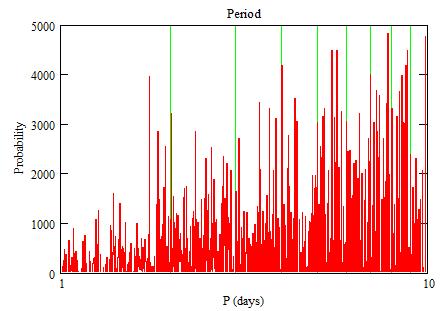
and the period:

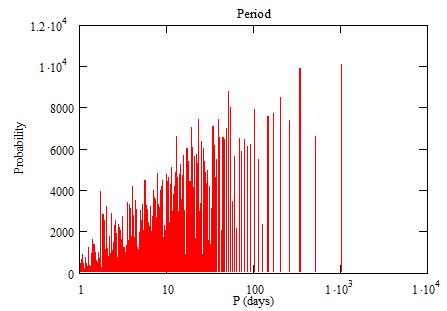
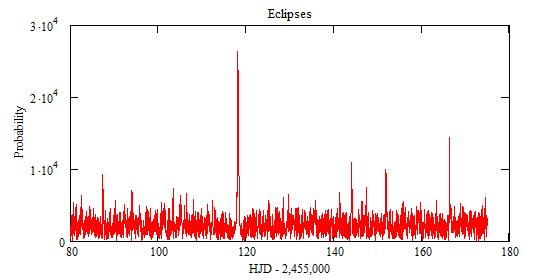
The probability for future eclipses may be computed:


However, the uncertainties et85 and et88 introduce an incertainty on their timing of (where t is the current time):
dt = et85+(et85+et88)*(t-t85)/(t88-t85)
dt = 0.48 day

Close-up:


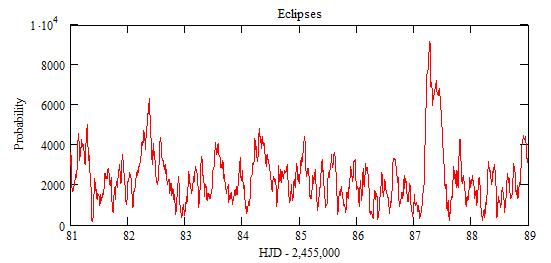
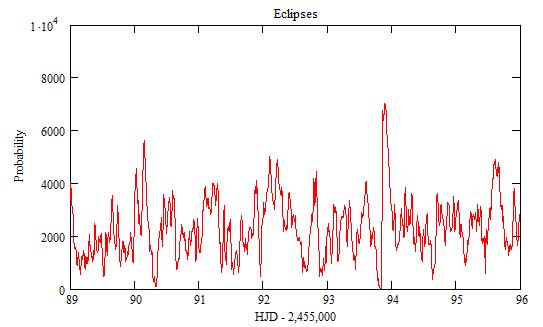
The small peaks correspond to n between 10 and 30. There is an incertainty of dt=0.48 on their position.






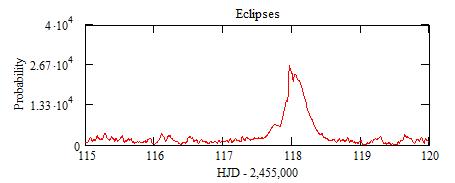
This large peak around 118 (12 Oct 2009) +/-dt=0.48 comes from values of n that are multiple of 3.

Other large periods:
n=1 and n=2: 455 THJD (15 Sep 2010)
n=4: 202 THJD (5 Jan 2010)
n=5: 253 THJD (25 Feb 2010)
n=7: 166 THJD (30 Nov 2009)
n=13: 143 THJD (8 Nov 2009)

Discussion

The minimum inclination of the orbit (so as to have an eclipse) may be estimated as:



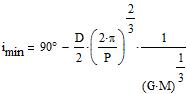
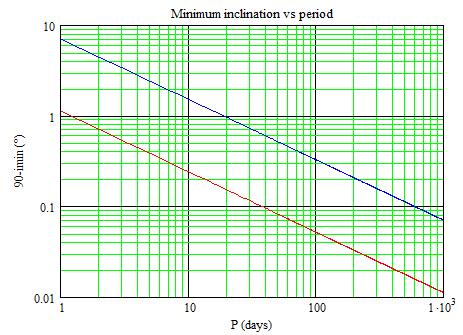
Red line: for D=1 and M=2; Blue line: for D=5 and M=1.

Long periods require an inclination of almost exactly 90° which would be a somewhat improbable coincidence.

References

Carilli C., Conner S. (1988) IAU Circ. 4648.

Landolt A.U. (1985) IAU Circ. 4125.

Zuckerman B., Becklin E. (1988) IAU Circ. 4652.