MBCAA Observatory

140 Siwa: light/rotation curves

Observed: Oct 2005-Feb 2006

Michel Bonnardeau
16 Dec 2005
Revised: 17 Dec 2005
Updated and revised 2 Apr 2009 with more data and a new analysis.

Abstract

Time-series are obtained for this asteroid. A period of rotation is searched using a Monte Carlo algorithm.

Introduction

Minor planet 140 Siwa orbits the Sun in 4.5 yr:

Siwa orbit according to the JPL.

Its absolute magnitude is H=8.34 mag, which suggests a diameter of about 110 km.

It is spining with a synodic period of P=18.495 h (Le Bras et al (2001)). However this does not seem to be well determined, as other observers have found different values.

Observations

The observations were carried out with a 203mm f/6.3 SC telescope, a Clear filter and a SBIG ST7E camera (KAF401E CCD). Each exposure is 1mn long.

Aperture photometry is performed for each image. The comparison stars differ for each session, as the asteroid is moving. The magnitude variations of Siwa are faint (maximum of about 0.1 mag). The choice of a Clear filter is then rather unfortunate (a red or BB filter would have improved the S/N). To get the most of the photometry, a stringent extra-losses software filter (Gary (2007)) is applied for each session, with a threshold of 0.1 mag. When a few images of a time-serie are below the threshold, they are discarded. When there are many of them below the threshold the whole time-serie is discarded.

An example of a light curve:

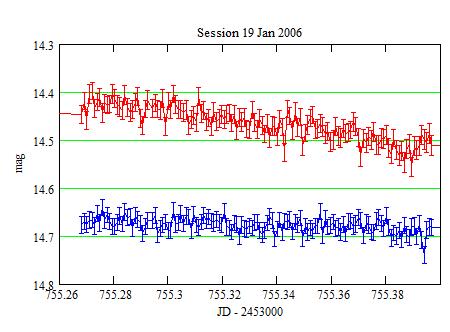
Red: Siwa, Blue: the check star. The error bars are +/- the 1-sigma statistical uncertainties.

and of the corresponding extra losses filter:

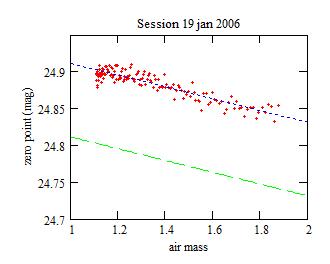
The points are expected to be along the blue line. The filter is the green line: the images that give zero points below it are discarded.

A résumé of the 9 usable sessions:

Session Nb. obs COMP star Check star

ID Average 1-sigma SD

10 Oct 2005 167 Ensemble photometry (6 COMP) UCAC2-34-394-008 = GSC-630-00771 0.028 0.033

20 Nov 2005 133 UCAC2-33-686-602 = GSC-34-00610 UCAC2-33-686-618 = GSC-35-01006 0.005 0.008

23 Dec 2005 52 UCAC2-33-863-903 = GSC-34-00823 UCAC2-33-863-894 = GSC-34-00762 0.007 0.012

19 Jan 2006 138 GSC-623-00208 UCAC2-34-768-974 = GSC-623-00395 0.017 0.018

22 Jan 2006 75 UCAC2-34-769-081 = GSC-633-00962 UCAC2-34-769-073 = GSC-623-00287 0.011 0.010

25 Jan 2006 152 UCAC2-34-954-388 = GSC-623-00962 UCAC2-34-954-376 = GSC-623-01295 0.033 0.035

31 Jan 2006 143 UCAC2-35-140-616 = GSC-630-00189 UCAC2-35-140-622 = GSC-630-00024 0.012 0.013

1 Feb 2006 148 UCAC2-35-140-661 = GSC-630-00066 GSC-630-00085 0.023 0.028

10 Feb 2006 119 UCAC2-35-509-740 = GSC-634-01182 UCAC2-35-509-738 = GSC-634-01215 0.022 0.023

The following sessions where discarded because of the extra losses filter:
23 Oct 2005
1 Nov 2005
24 Dec 2005
15 Jan 2006
20 Jan 2006
2 Feb 2006.

Futhermore, the session of 24 Jan 2006 was also discarded as the asteroid was moving across a crowded field.

Period search

The magnitude measurements are searched for a periodicity, which would be due to the asteroid spin.

For the first 2 sessions (10 Oct, 20 Nov 2005) the aspect of Siwa as seen from Earth and lighted by the Sun changes substantially. So these two sessions are not used in the period search. For the remaining 7 sessions, Earth is moving away from the asteroid which is seen with almost always the same aspect; see HERE diagrams of the Sun-Siwa-Earth geometry. The time of each measurement is corrected for the light time travel.

The variations of Siwa are faint but quite slow. The photometry measurements may then be grouped 4 by 4 to improve the S/N. This gives 208 measurements for the 7 sessions used in the period search.

To search for a periodicity I use a Monte Carlo algorithm the following way:

X X X

the magnitudes of the 6 last sessions are shifted so that their average magnitudes are the same as the one of first session. This is to take into account the dimming of the asteroid due mostly to the increasing Earth-Siwa distance;

the period is scanned from 12 h to 24 h with an increment of 2 s;

X
for each period, the phases of the observations are computed;

X
the observations are sorted by increasing phases;

X
the last 6 sessions have their magnitudes shifted by some numbers (different for each session) to take into account the fact that the comparison stars differ for each session, and that Siwa is varying. These numbers are taken randomly between 0.2 and -0.2 mag;

X X
the absolute values of the magnitude differences between 2 adjacent (in phase) measurements are summed, giving the "length" of the phase plot;

X X
this process of shifting the magnitudes by a set of random shifts is repeated 20,000 times;

X X
the set of magnitude shifts that gives the shortest phase plot length is retained;

the period that gives the shortest phase plot length is retained.

The above algorithm is re-run a 100 times. This does not lead to a unique period solution however, but rather to a spectrum strongly peaked around 19.6 hours:

The average value of the period from the 45 values in the strong peak is:
P = 19.7266 h +/- 18 s (the uncertainty is the standard deviation)

and the magnitude shitfs are:
19 Jan 2006  +0.020+/-0.006
22 Jan 2006  -0.104+/-0.008
25 Jan 2006  -0.027+/-0.006
31 Jan 2006  -0.118+/-0.007
01 Feb 2006  -0.002+/-0.006
10 Feb 2006  -0.020+/-0.006

The resulting phase plot:

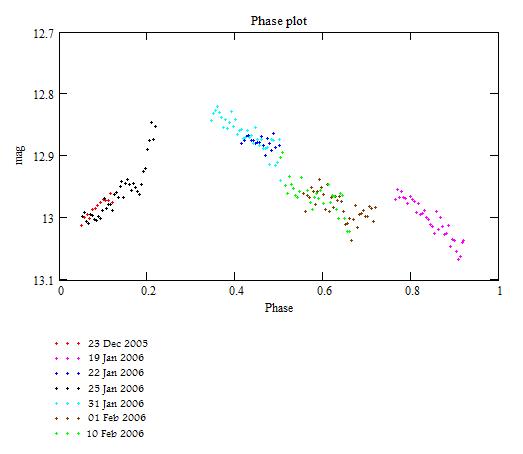
Discussion

What about the 2 time-series that were not used to determine the period (10 Oct, 20 Nov 2005)? Putting them on the phase plot gives:

Keeping in mind that the geometrical aspect was different of the sets used to derive the period, they may be considered as in agreement.

If the different time-series do not match very well, because of a changing geometry or of poor photometry, the Monte Carlo algorithm may tend to give longer periods. (If nothing match, the period will be as long as the whole observations).

A period of 18.495 h was derived by Le Bras et al (2001). When I fold my data with this period I do not get a realistic light curve, with 2 time-series at the same phase not being parallel.

A period of 17.16 h is reported on the R. Behrend's web site (as of March 2009). Actually I also find one solution (i.e. 1/100) at P=17.064 h. I get realistic light curves with these periods, but not as good looking as the one with the 19.7 h period.

The conclusion is that the period derived here is uncertain. Better observations would have been necessary, with the use of a filter and longer exposures, more measurements but spanning over a shorter time so as to have a fairly constant geometry.