MBCAA Observatory

TV Lib: temperature and radius variations from photometry

Observations: 11, 13, 17, 18 March 2005

Michel Bonnardeau
31 March 2005
Revised and Updated: 22 April 2005, 8 May 2005.

Abstract

Two-color time-series were obtained for this pulsating RR Lyrae star. The pulsation is too early when compared with the ephemeris. The temperature and the radius variations are computed from different models.

Introduction

TV Lib is a pulsating star with a period of 6.5 hours. It is classified as a RR Lyrae RRab with an asymmetric light curve.

However, this star is considered as "deviant": when compared with others RRab, its period is much smaller for its high metallicity (Bono et al (1997)).

Observations

The observations were carried out with a 203 mm SC telescope, Johnson B and V filters in a filter wheel and a SBIG ST7E camera (KAF401E CCD). The B and V filters are used alternatively. 95 images were obtained with the V filter and 94 with the B filter. Each exposure is 200 second long (except for two V exposures that are 60 s long).

The comparison star is Tycho 5581-00743 with Johnson magnitudes B=11.125 and V=10.303 (after conversion from the Tycho magnitudes, see Mamajek et al (2002)). The check star is GSC 5581-00764, with the observed magnitudes B=13.050 (standard deviation 0.081) and V=13.343 (0.015). A sample image is here.

The following light curve allows to time the pulse:

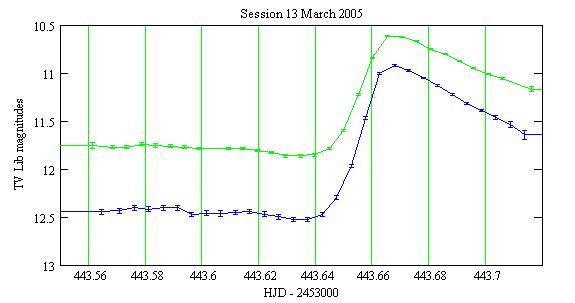
The error bars are the +/- one-sigma statistical uncertainties.

The pulse maximum is at: 2,453,443.665 HJD.
All the light curves, including those for the check star, are here.

Comparison with the ephemeris

The GCVS has a 91 yr old ephemeris for the pulse maxima:
T0 = 2,420,017.3015 (6 Sep 1913)
P0 = 0.269624031 day.

The pulse at 443.665 is then pulse number 123,974 and it should be at 443.671. It is 9 minutes too early.

Computation of the temperature

The temperature (°K) of the star surface may be estimated from the B-V magnitude owing to Reed (1998):

B-V = -3.684.log(T) + 14.551 (when T <9100°K)

I proceed the following way:

The measured magnitudes are folded in phase with the period P0. The B and V magnitudes are not measured simultaneously, therefore the magnitudes at any phase are computed by interpolation.

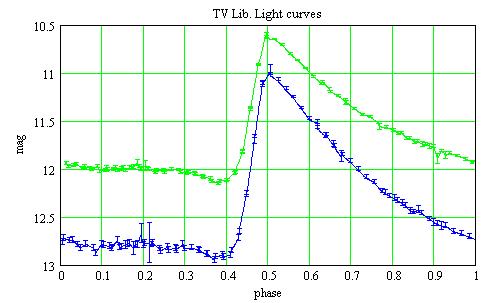
The measured magnitudes are corrected for the transformations coefficients:

B = b + Tb*Tbv*[(b - v) - (Bc - Vc)]
V = B - [(Bc - Vc) + Tbv*[(b - v) - (Bc - Vc)]]

where b, v are the measured magnitudes, Bc, Vc the magnitudes of the comparison star. Tb and Tbv are the transformations coefficients. They were measured on 7 Jan 2005 from the Landolt 95 field, of course with the same setup as for the present observation:

Tbv = 0.967
Tb = -0.043

The temperature versus the phase is then:

The red dot lines are the range of the temperatures corresponding to the +/- 1-sigma statistical uncertainties on the magnitudes. The thick red line is smoothed.

The distance

RR Lyrae stars are standard candles with all roughtly the same absolute average V magnitude of 0.6. With an observed average V magnitude of 11.531, the distance to TV Lib is then D=1.5kpc.

Layden (1997) has a more sophisticated distance estimation of D=1.42kpc.

Computations of the radius

I use 3 different methods to compute the star radius as a function of the phase:

The surface brightness method: Barnes and Evans (1976) considered a large number of measured star diameters (from occultation, interferometry, etc) and discovered an empirical relation between the diameter, the V magnitude, the B-V color. The star radius may then be computed, independantly of the temperature;

The bolometric method: I compare the absolute magnitude of the star with the one of the Sun. Knowing the radius of the Sun and the effective temperatures of the Sun and of TV Lib, I compute TV Lib radius;

The photon counting method: I assume the star radiates like a black body with the computed effective temperature. By counting the photons I detect at the telescope I compute the radius.

The radius from the surface brightness method

According to Barnes and Evans (1976) one has:

4.2207 -0.1*V -0.5*log(phi) = 3.964 - 0.333*(B-V)

where phi is the angular diameter in arc milliseconds. With the distance D=1420pc, the radius can readily be computed:

The dot lines are computed from the +/- 1-sigma statistical uncertainty on the magnitude. The thick line is smoothed.

The radius from the bolometric method

The absolute V magnitude Mv (at 10pc) of TV Lib may be computed from the measured V magnitude and the distance D=1420pc:

Mv = 5 + V - 5*log(D)

The Sun has an absolute V magnitude of Mov=4.89. The luminosity L(t) as a function of phase t of TV Lib is then (in Sun luminosity unit):

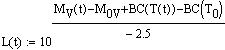
where To=5780°K is Sun effective temperature, and BC is the bolometric correction. BC as a function of the effective temperature is given by Reed (1998) as:

BC(T) = C6*(log(T)-4)^4 + C7*(log(T)-4)^3 + C8*(log(T)-4)^2 + C9*(log(T)-4) + C10
with C6=-8.499 C7=13.421 C8=-8.131 C9=-3.901 C10=-0.438.

The luminosity being proportional to R^2 and T^4, the radius R(t) is (in solar radii unit):

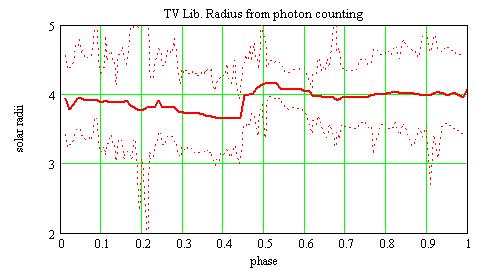
The radius from the photon counting method

Assuming the star radiates like a black body, the radius may be computed as a function of the distance to the star:

the number of photons Nv emitted by the star in the V band is, as a function of phase t and per unit of time (Stefan-Boltzmann law):

where:

R(t) is the star radius,
sigma is Stefan constant,
E is the energy of a photon in the V band: E=h.nu where h is the Planck constant and nu the photon frequency. nu=c/lambda where c is the velocity of light and lambda the wavelenght,
alpha(t) is the proportion of the energy emitted in the V band. alpha(t)=1 for the whole spectrum. It depends upon the phase t because is it T(t) dependant;

alpha(t) is given by:

where:

DELTAW(t) is the energy emitted by a black body in the frequency band DELTAnu,
k is Boltzmann constant,
W(t) is the energy emitted by a black body in the whole spectrum;

the number of photons received at the telescope (per unit of area and of time) is:

where:

nV(t) is the number of ADU counted by the camera (actually, the magnitudes are computed from this number),
g is the number of electrons/ADU. According to SBIG, g=2.3 for a ST7E camera,
qV=0.52 is the quantum efficiency of the CCD in the V band,
dzeta_t=0.8 is the telescope transmission,
dzeta_a=0.405 is the atmospheric transparency (it is assumed to be 0.7 for an air mass=1),
d1=203mm and d2=81mm are the diameters of the telescope and of the central obstruction,
tau=200s is the duration of one exposure;

the star radius R(t) over the distance to the star D is given by:

where Nv0(t) is Nv(t) for R=1 solar radius.

The V filter is centered at lambda=0.545micron. I make the simplification that its transmission curve is box-shaped with a width of 0.083micron and a height of 1. The star radius in solar radii for D=1.42 kpc is then:

Interstellar extinction

The interstellar extinction has not been taken into account. Its effect is to increase V and B-V. Correcting for the interstellar extinction would increase the computed temperature.

For the radius, correcting V would increase the radius, but the correction B-V is to diminish it. Therefore the interstellar extinction would have little effect on the radius computation. This was also noted by Barnes and Evans (1976).

Conclusions

One pulse is observed and found 9mn too early when compared with the 91-yr old ephemeris.

The temperature is found to increase when the star becomes brighter (from 5800 to 7200°K).

The computations of the radius with the surface brightness and the bolometric methods give a radius of 6 solar radii with an amplitude of 10%. The first method is independant of the temperature determination. The radius goes inwards just before the maximum of brightness and of temperature;

The computation of the radius with the photon counting method gives the same behavior as the other two methods, but with a smaller radius of 4 solar radii. This discrepancy may come from the star not being a black body, the atmospheric transparency being overated (I have an oceanic climate).