TX Mon: a Cepheid radius variations
Observed: 23 sessions from 29 Mar 2006 to 11 Mar 2007
Michel Bonnardeau
20 Jun 2007
Revised 29 Sept 2007 ("weighted" transformation coefficients)
Revised 29 Dec 2007 (improved transformations)
Abstract
B,V photometry measurements of this Cepheid are presented. The distance, temperature and radius of this pulsating star are computed.
Introduction
TX Mon is a classical Cepheid (a pulsating star) with a period of 8.7 days.
It was observed simultaneously with SZ Mon
as both stars are in the same field of view.
Observations
The observations were carried out with a 203mm f/6.3 SC telescope, B and V filters and a SBIG ST7E camera (KAF401E CCD). The comparison star is Tycho 4800-02165 with the Johnson magnitudes B=11.200 and V=11.094 (computed from the Tycho magnitudes with Mamajek et al (2002 & 2006)). The check star is GCS 4800-02059 with the measured magnitudes B=12.729 (standard deviation 0.062) and V=11.322 (0.012).
23 measurements were obtained with the B filter, 24 with the V filter. 2x20 measurements are pairs of nearly simultaneous B,V measurements, to be used to derive the B-V color. All the measurements are HERE.
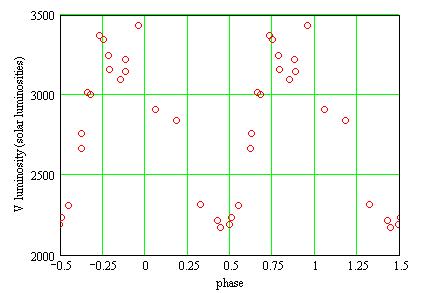
Phase plot
According to Andrievsky et al (2002), the ephemeris for the pulsation
is:
t(E) = T+E*P
with T = 2,452,242.80417 HJD (29 Nov 2001)
P = 8.70173 d
Folding my measurements with this ephemeris gives the phase plot:

Red: V magnitudes, Blue: B magnitudes. The error bars are +/- the
1-sigma statistical uncertainties.
The phase plot for the check star is HERE.
The pulse has a double peak and the ephemeris is for the second peak.
TX Mon was observed in 2003-2004 by ASAS
(Pojmanski (2002)) and in 1999-2000 by SkyDot/ROTSE-I/NSVS.
The data folded with the ephemeris are HERE.
There is not much evidence for a change of the pulsation in the last years.
However with the ephemeris of the GCVS:
TGCVS = 2,435,838.977 (31 Dec 1956)
PGCVS = 8.701731 d
TX Mon is now 0.1 period late from this 1956 ephemeris.
B-V color variation
There are 2x20 B,V measurements that are nearly simultaneous.
Then the phase plot of the B-V color:
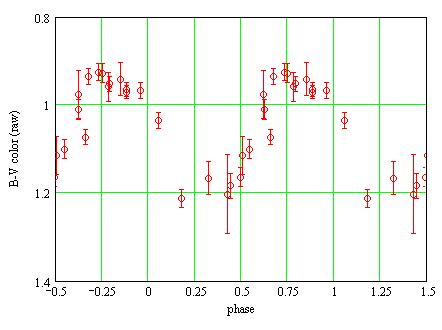
The measured b,v magnitudes may be transformed
for the instrument response. The transformed B,V magnitudes are then:
V = v + TvTbv*[(b-v)-(Bc-Vc)]
B = b + TbTbv*[(b-v)-(Bc-Vc)]
Bc,Vc are the magnitudes of the comparison star. The transformation coefficients
were measured HERE;
they are:
TbTbv = 0.002+/-0.027
TvTbv = -0.025+/-0.015
The transformed magnitudes are HERE. The
uncertainties on the transformed magnitudes are large because TX Mon and
the comparison star have very different colors (B-V~1, Bc-Vc=0.106).
The B-V phase plot with the transformed magnitudes:
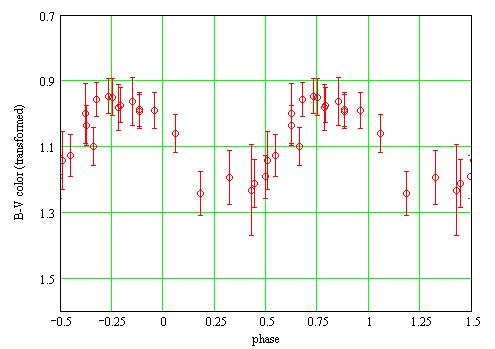
The B-V color as a function of the magnitude V is then:
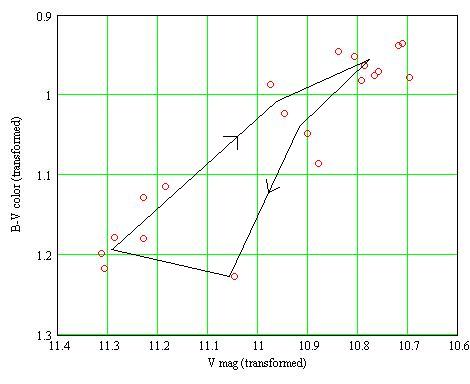
During the pulsation, the diagram is run along the black
line, in the direction of the arrows.
Distance
The absolute magnitude of a Cepheid can be computed from its period. By comparing it with the measured magnitude, the distance to the star can be inferred.
According to Tammann et al (2003) (equation (16)),
the absolute V magnitude MV is related to the period
P by:
MV=-3.141*log(P)-0.826
then MV=-3.777
I measured an average transformed V magnitude mV=10.949.
Tammann et al (2003) reports a measurement of the interstellar reddening
of E(B-V)=0.492. I evaluate the interstellar absorption as AV=R*E(B-V)
with R=3.1 for the Milky Way. Then AV=1.525 and the
distance is:
D= 10^(mV-AV-MV+5)/5
D= 4.4kpc = 14,000lyr
Temperature variation
According to Reed (1998) the effective temperature T (°K) can be computed
as a function of the B-V color:
B-V-E(B-V) = -3.684*log(T) + 14.551 (when T below 9100°K)
The effective temperature can then be computed as a function of the pulsational
phase:

Computations of the radius
I use 3 different methods to compute the star radius as a function of the phase:
Radius from the surface brightness method
According to Barnes and Evans (1976) there is the following empirical
relation between the angular diameter phi (in milliarcseconds), the V
magnitude and the B-V color:
4.2207 -0.1*(V-Av) -0.5*log(phi) = 3.964 - 0.333*(B-V-E(B-V))
With the distance, the radius can then be readily computed as a function
of the phase:
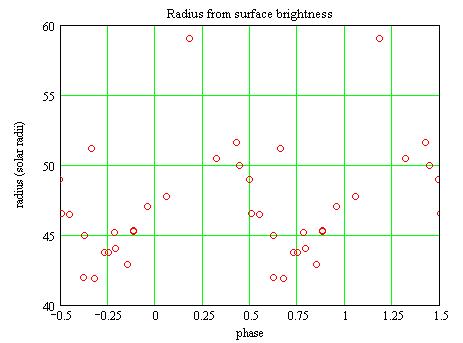
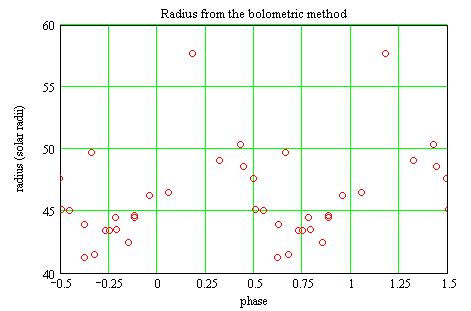
Radius from the bolometric method
The absolute V magnitudes Mv (at 10pc) may be computed from the measured
V magnitudes and the distance D:
Mv = 5 +(V-Av) - 5*log(D)
The luminosity L(t) as a function of phase tis then (in Sun luminosity
unit):
L(t) = 10^(Mv(t)-Mov+BC(T(t))-BC(To))/-2.5
where Mov=4.89 is the Sun absolute V magnitude, To=5780°K its effective
temperature, and BC is the bolometric correction. BC, a function of the
effective temperature, is given by Reed (1998) as:
BC(T) = C6*(log(T)-4)^4 + C7*(log(T)-4)^3 + C8*(log(T)-4)^2 + C9*(log(T)-4)
+ C10
with C6=-8.499 C7=13.421 C8=-8.131 C9=-3.901 C10=-0.438.
The luminosity as a function of the phase is then:
The luminosity being proportionnal to the square of the radius
and to the effective temperature to 4, the radius R(p) as a function
of the phase is then:
R(t) = (To/T(t))^2*sqrt(L(t))
in solar radii, with L(t) in solar luminosities:
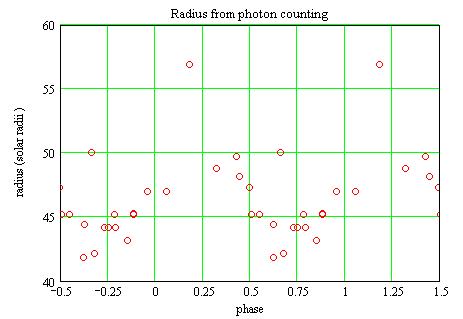
Radius from the photon counting method
Assuming the star radiates like a black body, the radius may be computed as a function of the distance to the star:
where:
- R(t) is the star radius,
- sigma is Stefan constant,
- E is the energy of a photon in the V band: E=h.nu where h is the Planck constant and nu the photon frequency. nu=c/lambda where c is the velocity of light and lambda the wavelenght,
- alpha(t) is the proportion of the energy emitted in the V band. alpha(t)=1 for the whole spectrum. It depends upon the phase t because is it T(t) dependant;
where:
- DELTAW(t) is the energy emitted by a black body in the frequency band DELTAnu,
- k is Boltzmann constant,
- W(t) is the energy emitted by a black body in the whole spectrum;
where:
- nV(t) is the number of ADU counted by the camera (actually, the magnitudes are computed from this number),
- g is the number of electrons/ADU. According to SBIG, g=2.3 for a ST7E camera,
- qV=0.52 is the quantum efficiency of the CCD in the V band,
- dzeta_t=0.8 is the telescope transmission,
- dzeta_a=0.4 is the atmospheric transparency (I adjusted this parameter so that I get the same radius as with the other 2 methods),
- d1=203mm and d2=81mm are the diameters of the telescope and of the central obstruction,
- tau=200s is the duration of one exposure;
where Nv0(t) is Nv(t) for R=1 solar radius.
The V filter is centered at lambda=0.545micron. I make the simplification
that its transmission curve is box-shaped with a width of 0.083micron
and a height of 1. The star radius in solar radii for the distance D=4.4kpc
is then:
Discussion
The 3 methods for the determination of the radius give roughtly the same results, although there are quite different. However, for the photon counting method, as I do not know the atmospheric transparency, I ajusted it to dzeta_a=0.4 so as to obtain the same result as with the other 2 methods. With an average airmass of 1.51 this corresponds to an atmospheric extinction of 0.659mag/airmass at 5450A.
According to King (1985) the atmospheric extinction for a dust free atmosphere is 0.1020mag/airmass at 5450A.
The difference may come from my atmosphere not being that transparent (my climate is oceanic) and also from the assumption that the star is a perfect back body being too crude.
References
Andrievsky S.M., Kovtyukh V.V., Luck R.E., Lepine J.R.D., Maciel W.J., Beletsky Y.V. (2002) A&A arXiv:astro-ph/0208056.
Barnes T.G., Evans D.S. (1976) MNRAS 174 489.
King D.L. (1985) Atmospheric extinction at the Rogue of Muchachos Observatory, La Palma RGO/La Palma technical note n° 31.
Mamajek E.E., Meyer M.R., Liebert J. (2002) AJ 124 1670 Appendix
C;
erratum (2006) AJ 131 2360.
Pojmanski G. (2002) Acta Astronomica 52 397.
Reed C. (1998) J. RAS of Canada 92 36.
Tammann G.A., Sandage A., Reindl B. (2003) A&A arXiv:astro-ph/0303378.
Acknowledgement
This amateur research has made use of SkyDot/ROTSE-I/NSVS data.
Technical notes
Telescope and camera configuration.
Computer and software configuration.
Transformations for differential photometry.
Transformation coefficients: B, V measurements.
Astronomical notes
Pulsating stars and its links.
SZ Mon (a RV Tau star) in the same field of view.
Other determinations of temperature and radius of pulsating stars.
|
|
|||
|
|||
|
|
|||
|
|
|||
|
|||
