MBCAA Observatory

V1412 Aql: a simulation

Michel Bonnardeau
First version 24 Aug 2009
Updated 2 Sep 2009 (more observations)
Updated and corrected 3 Sep 2009 (more observations; uncertainties on the ToM of the 2 eclipses taken into account at the suggestion of Wolfgang Renz; correction of the number of solutions)
Updated 5 Sep 2009 (more observations; simulation with the period down to 1 d; inclination)
Corrected 10 Sep 2009 (uncertainties on the ToM of the 2 eclipses)
Updated 15 Sep 2009 (more observations)
Updated 20 Sep 2009 (more observations, slightly different ranges for the simulation)
Updated 21 Sep 2009 (inclination taken into account in the Monte Carlo)
Updated 25 Sep 2009 (more observations, smaller mass range and cos(i) at the suggestion of Christian Knigge)

Abstract

A Monte Carlo simulation which may be useful to search for eclipses is proposed.

Introduction

The white dwarf G24-9 (or V1412 Aql) was observed to be unexpectedly faint on 2 occasions, in 1985 and 1988. This is interpreted as eclipses due to a dark, substellar companion (Zuckerman & Becklin (1988)).

According to Bergeron et al (2001) G24-9 has a parallax of 0.0447" (then a distance of 22.4 pc), a temperature of 6400°K, a mass M=0.65+/-0.04 solar mass, a gravity g=10^8.13cm/s2 (then a radius sqrt(G*M/g)=8018km).

Feb 2009, the AAVSO lauched a campaign to observe this object so as to detect its eclipses (AAVSO Special Notice #148).

I propose here a Monte Carlo simulation which may be useful to speed up the discovery of eclipses.

Observations

The 2 observed eclipses are:

19851007.11 (Landolt (1985)), heliocentric correction 180.56s, t85=2,446,345.612 HJD. The uncertainty is taken as et85=0.005 HJD;

19880715.3 (Carilli & Conner (1988)), heliocentric correction 441.74s, t88=2,447,357.805 HJD. The uncertainty is taken as et88=0.05 HJD.

The AAVSO has 1116 negative (i.e. no eclipse) observations on 15 Sep 2009.

Arne Henden obtained 14 time-series showing no eclipses, from 30 Oct to 8 Dec 2008, total duration 34.1 h. And also 7 short time-series, in 2002 and 2008, total duration 2.6h.
Robert Fridrich obtained a time-series on 1 Sep 2009, duration 0.3 h.

Christian Knigge also obtained 329 negative measurements in 2009.

Simulation

The orbital period is P=(t88-t85)/n=(1012.193 days)/n where n is an integer (assuming it is constant, i.e. no mass transfer, no third body).

G29-4 is a white dwarf, so it has a small size (about that of Earth), then the eclipse duration tau is given mostly by the diameter D of the occulting body:

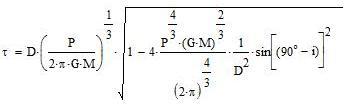
with M the mass of the system, i the inclination, G the gravitational constant (taking for the eccentricity e=0).

The computer simulation is a Monte Carlo one where a large number of random sets of n, M, D, i are used to derived ephemeris. The ephemeris that are retained are those that give the 2 observed eclipses and that do not give eclipses for the negative observations (with i large enough to give an eclipse).

The algorithm works the following way:

  • 100,000,000 random sets of n, M, D, i are generated, with n between 1 and 1000, M between 0.57 and 0.80 solar masses (2 sigma uncertainty for the white dwarf, and up to 0.07 for the occulter (a brown dwarf)), D between 0.15 and 5 jovian diameters,cos(i) between cos(85°) and 0;
  • when i is too small for an eclipse to occur, the set is rejected;
  • for each set the period P0=(t88-t85)/n and the eclipse duration tau is computed;
  • the ephemeris is HJD(E)=T+P*E with T an random number between t85-tau and t85+tau, and P a random number between P0-tau/n and P0+tau/n;
  • the ephemeris than do not give the eclipses at t85 and t88 are rejected;
  • the ephemeris that give an eclipse for one of the negative observations or for one of the 14+7+1 time-series are rejected.

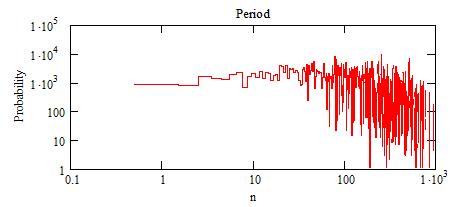
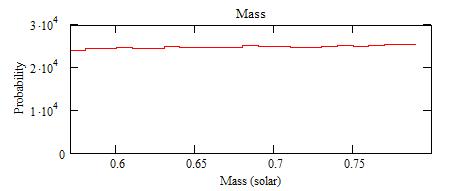
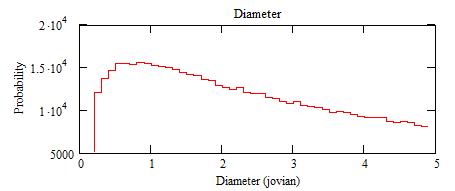
    • The spectra of n, M, D and i solutions are:



    The "probability" is actually the number of acceptable solutions from the simulation.




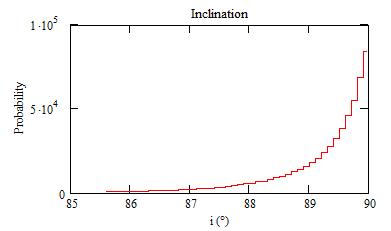
    The average for the inclinations is 89.3°.

    The probability for the eclipse duration:


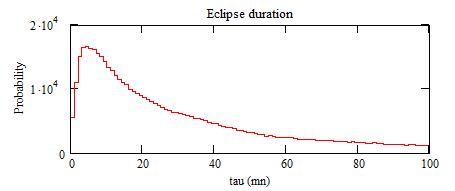
    The average for the eclipse durations is 41 mn.

    and the period:



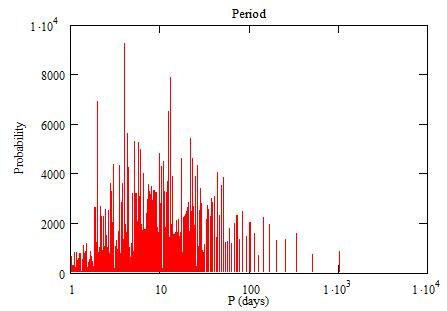
    The average for the periods is 18 days.

    The probability for future eclipses may be computed:



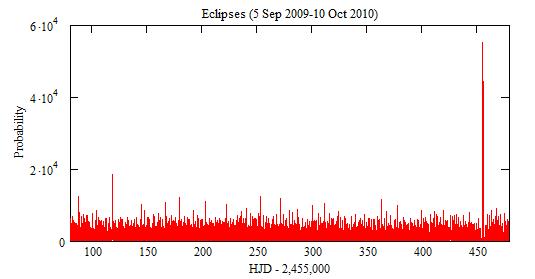
    However, the uncertainties et85 and et88 introduce an uncertainty on their timing of (where t is the current time):
    dt = et85+(et85+et88)*(t-t85)/(t88-t85)
    dt = 0.48 day

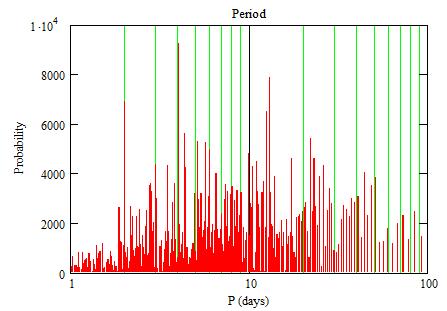
    Close-up:




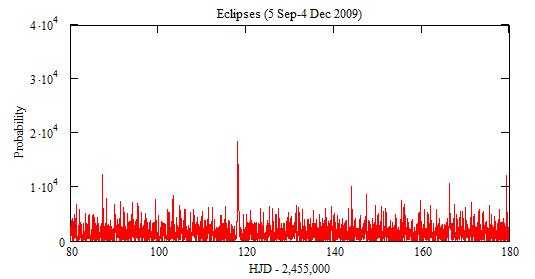
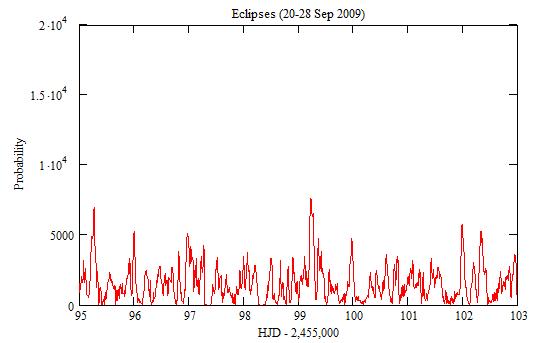
    The small peaks correspond to short periods. There is an uncertainty of dt=0.48 on their position.






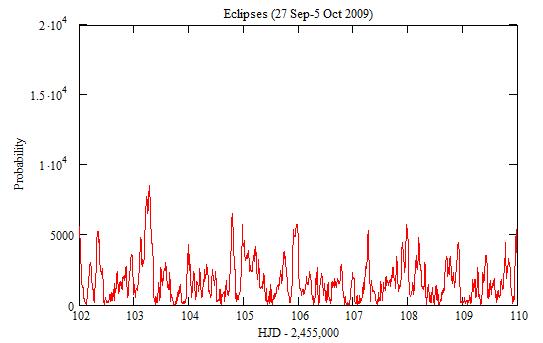
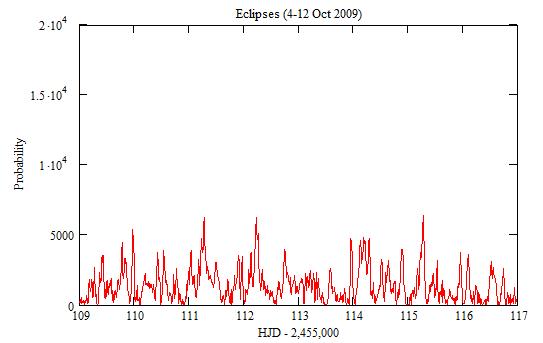
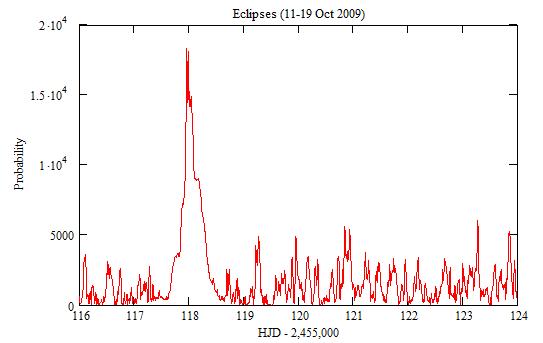
    The large peak around 118 (13 Oct 2009) comes from values of n that are multiple of 3. Because of the uncertainty dt=0.48, one needs time-series from 117.0 to 119.0 to check it.

    Other (than n=3) large periods:
    n=1 and n=2: 455 THJD (15 Sep 2010)
    n=4: 202 THJD (5 Jan 2010)
    n=5: 253 THJD (25 Feb 2010)
    n=7: 166 THJD (30 Nov 2009)
    n=11: most of it eliminated by the time-series
    n=13: 143 THJD (8 Nov 2009)

    Discussion

  • The peaks correspond to possible long periods and they can be checked by time-series.
  • Outside the peaks, the probabilities are not nil, and correspond to short periods. They can be checked by single measurements (or time-series) and by having some luck.
  • Periods below 1 day are now eliminated by the time-series.

    • References

    Bergeron P., Leggett S.K., Ruiz M.T. (2001) ApJ Supp 133 413.

    Carilli C., Conner S. (1988) IAU Circ. 4648.

    Landolt A.U. (1985) IAU Circ. 4125.

    Zuckerman B., Becklin E. (1988) IAU Circ. 4652.



    Site map

    Search

    Copyright notice
    &
    Contact

    .
    http://www.astromb.net
    MBCAA Observatory. Copyright 2004-2009