V1412 Aql: a simulation
Michel Bonnardeau
First version 24 Aug 2009
Updated 2 Sep 2009 (more observations)
Updated and corrected 3 Sep 2009 (more observations; uncertainties on
the ToM of the 2 eclipses taken into account at the suggestion of Wolfgang
Renz; correction of the number of solutions)
Updated 5 Sep 2009 (more observations; simulation with the period down to 1 d;
inclination)
Corrected 10 Sep 2009 (uncertainties
on the ToM of the 2 eclipses)
Updated 15 Sep 2009 (more observations)
Updated 20 Sep 2009 (more observations, slightly different ranges for
the simulation)
Updated 21 Sep 2009
(inclination taken into account in the Monte Carlo)
Updated 25 Sep 2009 (more observations, smaller mass range and cos(i) at the
suggestion of Christian Knigge)
Updated 11 Oct 2009 (better timing
for the 1985 eclipse)
Updated 21 Oct 2009 (more observations)
Updated 30 Oct 2009 (more observations)
Abstract
A Monte Carlo simulation which may be useful to search for eclipses is proposed.
Introduction
The white dwarf G24-9 (or V1412 Aql) was observed to be unexpectedly faint on 2 occasions, in 1985 and 1988. This is interpreted as eclipses due to a dark, substellar companion (Zuckerman & Becklin (1988)).
According to Bergeron et al (2001) G24-9 has a parallax of 0.0447" (then a distance of 22.4 pc), a temperature of 6400°K, a mass M=0.65+/-0.04 solar mass, a gravity g=10^8.13cm/s2 (then a radius sqrt(G*M/g)=8018km).
Feb 2009, the AAVSO lauched a campaign to observe this object so as to detect its eclipses (AAVSO Special Notice #148).
I propose here a Monte Carlo simulation which may be useful to speed up the discovery of eclipses.
Observations
The 2 observed eclipses are:
19851007.11 (Landolt (1985)), t85=2,446,345.61828 HJD (C. Knigge, personal
communication). The uncertainty is considered as negligeable et85=0;
19880715.3 (Carilli & Conner (1988)), heliocentric correction 441.74s,
t88=2,447,357.805 HJD. The uncertainty is taken as et88=0.05 HJD.
The AAVSO has 1328 negative (i.e. no eclipse) observations on 30 Oct 2009.
Arne Henden obtained 14 time-series showing no eclipses, from 30 Oct to
8 Dec 2008, total duration 34.1 h. And also 7 short time-series, in 2002
and 2008, total duration 2.6h.
Robert Fridrich obtained a time-series on 1 Sep 2009, duration 0.3 h.
Christian Knigge also obtained 478 negative measurements in 2009.
Simulation
The orbital period is P=(t88-t85)/n=(1012.187 days)/n where n is an
integer (assuming it is constant, i.e. no mass transfer, no third body).
G29-4 is a white dwarf, so it has a small size (about that of Earth),
then the eclipse duration tau is given mostly by the diameter D of the
occulting body:

with M the mass of the system, i the inclination, G the gravitational
constant (taking for the eccentricity e=0).
The computer simulation is a Monte Carlo one where a large number of random sets of n, M, D, i are used to derived ephemeris. The ephemeris that are retained are those that give the 2 observed eclipses and that do not give eclipses for the negative observations (with i large enough to give an eclipse).
The algorithm works the following way:
The spectra of n, M, D and i solutions are:

The "probability" is actually the number of acceptable solutions from
the simulation.



The average for the inclinations is 89.3°.
The probability for the eclipse duration:

The average for the eclipse durations is 39.4 mn.
and the period:


The average for the periods is 19.5 days.
The probability for future eclipses may be computed:

However, the uncertainties et85 and et88 introduce an uncertainty on their
timing of (where t is the current time):
dt = et85+(et85+et88)*(t-t85)/(t88-t85)
dt = 0.44 day
Close-up:

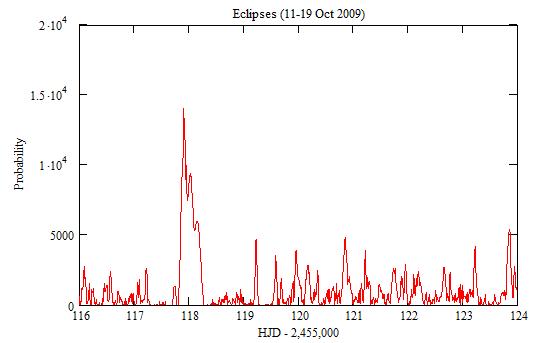
The large peak around 118 (13 Oct 2009) comes from values of n that
are multiple of 3.

The small peaks correspond to short periods. There is an uncertainty
of dt=0.44d on their position.
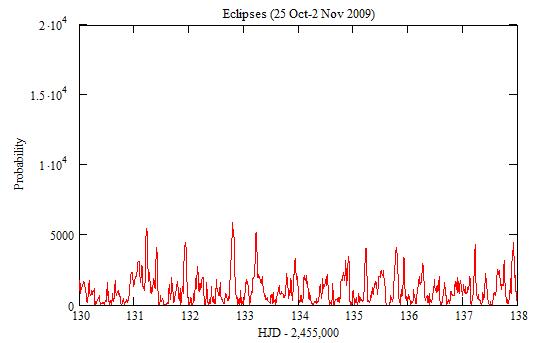





Other (than n=3) large periods:
n=1 and n=2 (actually whatever n is): 455 THJD (15 Sep 2010)
n=4: 202 THJD (5 Jan 2010)
n=5: 253 THJD (25 Feb 2010)
n=7: 166 THJD (30 Nov 2009)
n=11: most of it eliminated by the time-series
n=13: 143 THJD (8 Nov 2009)
Discussion
Whatever n is, there should be an eclipse around 15 Sep 2010. Time-series during a few days around that date should catch it.
It would be interestingl to do radial velocity measurements (by spectroscopy).
References
Bergeron P., Leggett S.K., Ruiz M.T. (2001) ApJ Supp 133 413.
Carilli C., Conner S. (1988) IAU Circ. 4648.
Landolt A.U. (1985) IAU Circ. 4125.
Zuckerman B., Becklin E. (1988) IAU Circ. 4652.
|
|
|||
|
|||
|
|
|||
|
|
|||
|
|||
